前缀和
前缀和是一种预处理技术,通过计算数组中每个位置前所有元素的和,可以快速求出任意区间的和。
前缀和的核⼼思想是预处理,可以在暴⼒枚举的过程中,快速给出查询的结果,从⽽优化时间复杂度,是经典的⽤空间替换时间的做法。
一维前缀和
实现原理
对于数组 arr,构建一个前缀和数组 prefix,其中:
prefix[0] = 0prefix[i] = arr[0] + arr[1] + ... + arr[i-1]
代码实现
// 构建前缀和数组 function buildPrefixSum(arr) { const n = arr.length; const prefix = new Array(n + 1).fill(0); for (let i = 0; i < n; i++) { prefix[i + 1] = prefix[i] + arr[i]; } return prefix; } // 查询区间和 [l, r] function queryRangeSum(prefix, l, r) { return prefix[r + 1] - prefix[l]; } // 示例 const arr = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]; const prefix = buildPrefixSum(arr); console.log("前缀和数组:", prefix); // [0, 1, 3, 6, 10, 15, 21, 28, 36, 45, 55] console.log("区间 [2, 5] 的和:", queryRangeSum(prefix, 2, 5)); // 21 - 3 = 3 + 4 + 5 + 6 = 18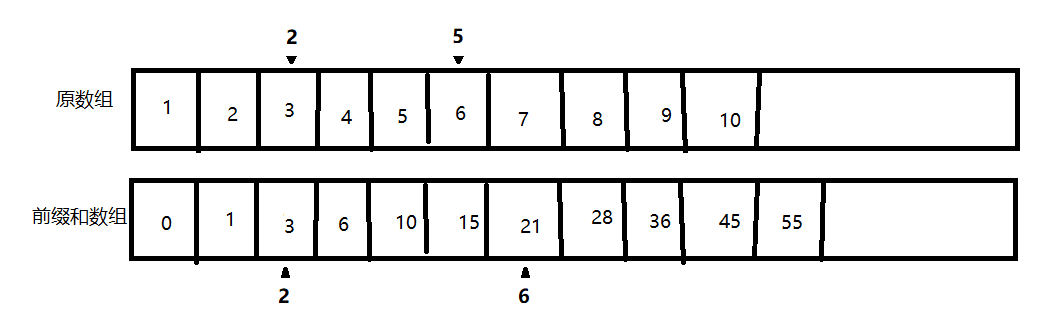
前缀和图解复杂度分析
- 时间复杂度
- 预处理:
O(n) - 查询:
O(1)
- 预处理:
- 空间复杂度:
O(n)
- 时间复杂度
算法优势
- 暴力法:每次查询时间复杂度为
O(n),m 次查询为O(mn) - 前缀和法:预处理时间复杂度为
O(n),每次查询为O(1),m 次查询为O(m);需要额外的O(n)空间存储前缀和数组
- 暴力法:每次查询时间复杂度为
二维前缀和
M-原始数组,P-前缀和数组
预处理:
P[i][j] = M[i-1][j-1] + P[i-1][j] + P[i][j-1] - P[i-1][j-1]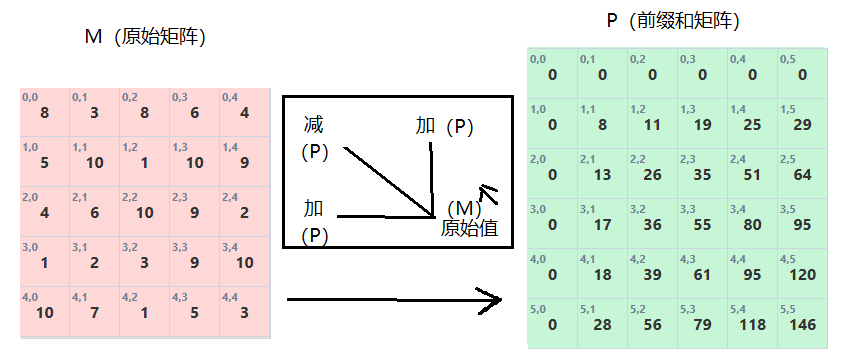
二维前缀和矩阵图解查询:查询 (r1,c1) 到 (r2,c2) 区域和
sum = P[r2+1][c2+1] - P[r1][c2+1] - P[r2+1][c1] + P[r1][c1]
二维前缀和查询图解代码实现
// 生成随机矩阵
function generateRandomMatrix(size, maxValue) {
const matrix = [];
for (let i = 0; i < size; i++) {
const row = [];
for (let j = 0; j < size; j++) {
row.push(Math.floor(Math.random() * maxValue) + 1);
}
matrix.push(row);
}
return matrix;
}
// 构建二维前缀和矩阵
function buildPrefixMatrix(matrix) {
const n = matrix.length;
const m = matrix[0].length;
const prefix = Array(n + 1).fill().map(() => Array(m + 1).fill(0));
for (let i = 1; i <= n; i++) {
for (let j = 1; j <= m; j++) {
prefix[i][j] = matrix[i-1][j-1] + prefix[i-1][j] + prefix[i][j-1] - prefix[i-1][j-1];
}
}
return prefix;
}
const matrix = generateRandomMatrix(5, 10);
console.log("原始矩阵:", matrix);
const prefixMatrix = buildPrefixMatrix(matrix);
console.log("前缀和矩阵:", prefixMatrix);
const r1 = 1, c1 = 1, r2 = 3, c2 = 3;
const sum = prefixMatrix[r2+1][c2+1] - prefixMatrix[r1][c2+1] - prefixMatrix[r2+1][c1] + prefixMatrix[r1][c1];
console.log(`区域 (${r1},${c1}) 到 (${r2},${c2}) 的和为:${sum}`);